Разбор Современной кинематики равноускоренного движения.

 

 

 

 

 

Цитата взята из «Элементарный  учебник Физики»  под редакцией Г.С. Ландсберга. Том 1. Механика….

 

Отметим, что  при Галилее  не было секундомеров, и в качестве замены оного он использовал достаточно точный эквивалентный способ, не уступающий и современным методикам при наличии достаточно хороших весов, в наличии которых у него в арсенале не приходится сомневаться!!!!!

 

Итак, Галилей установил пропорциональность пути квадрату времени  движения.  Вроде бы ничего особенного, если не смотреть на современную формулу для равноускоренного движения с места.

 

S=at²/2    а-const

 

Где данная пропорция по какой-то причине  уменьшилась вдвое!!!!  Что никак не спишешь на несовершенство метода измерения, использованного Галилеем, и не спишешь на то,  что он не учел трения. Так как  в процессе опытов изменялся угол наклона желоба и сильного  (в 2 раза!!!) отклонения от обнаруженной закономерности  при различных углах замечено не было!!!

 

Есть умники, которые, глядя на данный текст, сразу встают на дыбы и кричат о непонимании разницы между пропорциональностью и знаком равенства.

Но, боже мой! Какая разница между временем и ускорением, если ускорение –величина постоянная!!!! Что одно делить на двойку, что второе, смысл пропорции не меняется.  Меняется ее величина. То есть нарушается пропорциональность. Таким образом, занижается ускорение, а пропорциональность квадрату времени остается.

 

 

Упоминаний о других подобных опытах в литературе не встречается. 

Зато имеются многочисленные математические и геометрические «подтверждения» приведенного выражения, приходящие в противоречие с пропорциональностью, полученной Галилеем.

 

Такое же противоречие обнаруживается и при вычислении скорости по формуле  V=at,   где ускорение должно вычисляться, а не подставляться в виде исходных данных, поскольку само зависит от изменения скорости движения.

 

a=(v1-v0)/t           и  с учетом   v=s/t           a=(s1/t-s2/t)/T  где  Т-общее время движения.

 

 

Корни этой ошибки лежат в сугубо математическом подходе к физическому процессу. Математика не принимает в учет непрерывности движения и сваливается в сторону замены равноускоренного движения на равномерное, в случае малых отрезков пути и времени их преодоления.   Причем даже не маскирует эту подмену, явно замечая,

 

 

 

 

А что такое средняя скорость? это скорость в предположении равномерного движения.  Любой современный спидометр показывает скорость предполагаемого равномерного движения в дальнейшем, а не историю движения вообще. И это не мгновенная скорость, поскольку в физике ничего мгновенно не делается.

То есть, заменяя физику в малом, все более врем в большом.

 

Часто пытаются парировать:

-----------------------------------

Дело в том, что в современной формуле S=at^2/2 путь тоже пропорционален t^2

----------------------------------

Не вы первый.

Галилей не имел дела со средними скоростями, у него скорость  v=s/t.

 

замечу, для равноускоренного движения. он только подбирался к ускорению.

отсюда и нормальная пропорция, ни ускорение, ни время пополам не делится.  ОН же не знал позднейшего способа описать равноускоренное движение при помощи равномерного. <smile type=":)">

что проще для математика? свое мнение, а не природа. ввел среднее и не позаботился, что физический процесс то непрерывен. взял малый интервал и поделил пополам, сказал среднее.

Все поверили.   АВТОРИТЕТ.

работа Гюйгенса, больше некому.

 

а вот теперь имеются графики такого вида

 

 

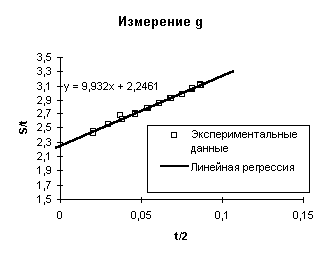
спрашивается  откуда там t/2?

а это чтоб тангенс угла наклона прямой  соответствовал принятому ускорению свободного падения...9.8.  по Гюйгенсу!!!  Стоит задуматься, а чему на самом деле равно ускорение свободного падения????!!!!.  Ровно в два раза больше!!!!   Тангенс угла наклона прямой—это определение ускорения как отношения скорости к времени, но никак не к его половине t/2 .

 

Для начала рассмотрим школьный курс и методику доказательства.

 

Геометрический способ.

 Вот смотрим, как это дано в учебнике: кстати время на оси представленного ниже графика отложено в соответствии с определением!!!!

При равноускоренном прямолинейном движении скорость тела определяется формулой

υ = υ0 + at.

(*)

В этой формуле υ₀ – скорость тела при t = 0 (начальная скорость), a = const – ускорение. На графике скорости υ(t) эта зависимость изображается прямой линией.

 

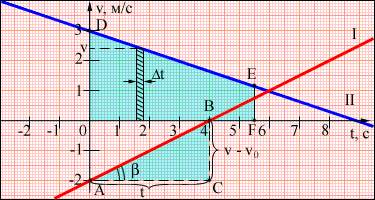
По наклону графика скорости может быть определено ускорение a тела. Соответствующие построения выполнены на рис.  для графика I. Ускорение численно равно отношению сторон треугольника АВС:

Чем больше угол β, который образует график скорости с осью времени, т. е. чем больше наклон графика (крутизна), тем больше ускорение тела.

Для графика I: υ₀ = –2 м/с, a = 1/2 м/с².

Для графика II: υ₀ = 3 м/с, a = –1/3 м/с².

 

Комментарий.

Отрицательная скорость в приведенном примере уже абсурд в физике.  Ни времени, ни пути отрицательных не бывает.

Часы в обратную сторону не ходят, а может только измениться на противоположное направление движения, и то с оговорками для движущегося тела, обладающего массой (перед изменением направления движения необходимо уменьшить скорость до нуля. То есть двигаться равнозамедленно в нашем случае).

а=tg β=(v-v₀)/t =  a=s/t²    определение ускорения!!!!

 

Заметим, что при движении с места  v0=0   и  a=v/t,  s=vt

 

 

Наклонная линия или гипотенуза АВ  треугольника АВС является геометрическим местом Точек  Ускорения. 

а=tg β=(v-v0)/t    = Сonst.

Из любых точек гипотенузы можно построить подобные треугольники, где данное отношение и является постоянным а=tg β

Таким образом,  представленная на графике наклонная линия   содержит в любом своем месте точку,  являющуюся константой, равной ускорению. a =v/t

Многие называют это графиком скорости, хотя это график(изменения скорости, а это и есть ускорение) отношения скорости к времени и  в случае переменного изменения( нелинейного изменения скорости) может иметь любой вид, хотя бы синусоидальный.

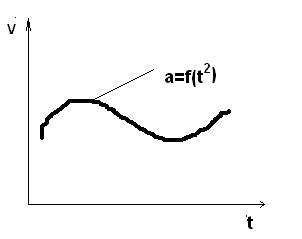
Если рассматривать в общепринятом понимании зависимость скорости от времени,  то  она  сама является функцией отношения  v=f(t)=s/t 

Классическое понимание в координатном изображении, и например, график прямой линии предусматривает уравнение  ax+by+-c=0 , где каждой точке на оси y  соответствует точка на оси x. В данном случае то ли намеренно, то ли вообще от полного незнания геометрии и математики совершено совмещение линейной и обратно пропорциональной зависимости.

 s=vt=s!!!!!!!

Таким образом графика зависимости скорости от времени не получить вообще!!!!!!

Поскольку произведение можно представить только в виде площади, но никак не графика.

Проекции отрезка данной линии на любую из осей графика не существует.

 

а-а=0   и   соответственно  нулю равна любая проекция. 

Из данного графика  можно определить скорость в любой момент времени при заданном ускорении.

 

По формуле   а=v/t

Либо время по той же формуле.

 

То есть данный график отражает отношение скорости к времени, а не их произведение.  Собственно это линия постоянного Ускорения.

 

 

Имеется еще один пример подобной зависимости из электротехники.

Это знаменитая вольтамперная характеристика.

Она отражает закон Ома

I=U/R

А в графическом отображении имеет два варианта.

1 вариант зависимость тока от напряжения

 

 

2 вариант зависимость напряжения от тока.

Два разных исполнения, обзываемых одним словом-«вольт-амперная характеристика» и два разных физических смысла.

R=U/I   сопротивление  среды

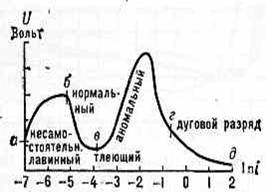
Пример—электрический разряд в газах

 

1/R=I/U  Проводимость среды

 

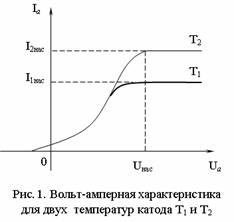электровакуумный диод

 

Однако, продолжим…

Несмотря на данные особенности представления зависимости скорости от временив в виде отношения,  в учебнике пишут:

«График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt.»

 

 

А ПОЧЕМУ ЭТО ОДНО ФИЗИЧЕСКОЕ ДЕЙСТВИЕ ПОДМЕНЯЕТСЯ ДРУГИМ??? Как мало не делить непрерывный физический процесс ускоренного движения от этого оно ускоренным быть не перестанет. И математическое допущение физики не изменит. Только точность падает однозначно..

« Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной на рис. 1.4.2 полоски. Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, можно получить, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены на рис. 1.4.2 для графика II. Время t принято равным 5,5 с.

(1)

 

 

Так как υ – υ₀ = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

 

S=v₀t+at²/2

-----------------------------------------------------------------------------«»»»»»конец выдержки

Таким образом, никакого перемещения и его проекции на ось времени не существует. Перемещение или путь при равноускоренном движении определить из данного графика напрямую невозможно.

 

Можно просто алгебраически помножить скорость на время и получить площадь прямоугольника, численно равную величине пройденного пути по заданным значениям. А это  уже не геометрия.

 

Следует отметить,  что после рассуждений о «проекции»  появляется еще более  ошеломляющая физичностью фраза, отмеченная красным  цветом.

По волшебству   ДОКАЗУЮЩЕГО    равноускоренное движение путем  среднего оболванивания словами превращается в равномерное!!!!!!!

 

Далее начинаются последствия такой геометрии.

 

Алгебраическая подстановка при нулевой начальной скорости v0 и v=s/t, a=s/t2 в выражение (1)  приводит к элементарной ошибке  s=s/2     вместо обращения в ноль обоих частей уравнения.

Один из оппонентов прямо сказал, пытаясь как то возразить на очевидную вещь:

«полметра за сек пробежишь только если скорость всю сек равна пол метра в сек, а если скорость в начале ноль, а только в конце полметра в сек, то пробежишь меньше.»

Хочу и бегу с места пол метра за секунду, да и сколько угодно могу пробежать, с секундомером, по линейке, а мне запрещают, говорят что бежишь меньше, мало того в два раза!!!!!!во!

А я, что интересно, пробегаю с места эти полметра за положенное время, оглядываюсь назад… и не пробежал?  Пробежал, с секундомером все в порядке, да и  с расстоянием тоже, линейка короче не стала.

Очевидный вывод:    Геометрическое обоснование неудачно. Результат путаницы между графическим представлением функции  у=f(x) и графическим преставлением отношения.

 

То есть v=s(t)=s/t,    a=v(t) = v/t=v/t²

И в графическом представлении равноускоренного движения нет особой необходимости.

 

Если рассматривать ускоренное движение в общем виде, такой график необходим только для качественного объяснения движения с функциональной зависимостью изменения скорости.

 

И не стоит забывать, что это отношение a=v/t=s/t2

 

Одно из последствий:   При отрицательном ускорении – торможении:

время можно задавать в качестве начального условия  ровно в два раза большее, чем это требуется для осуществления самого движения. Причем расчетный путь оказывается положительным, и только при превышении двойного значения времени становится отрицательным. Таким образом, не отслеживается конечность процесса, а путь будет мнимым.

 

 

Далее рассмотрим один простой, прямо таки жизненный пример, взятый из спорта,

Подсказанный одним из оппонентов сообщества «Физика»  на mail.ru (Вячеслав Галкин)

 

Данный опыт является подтверждением, представленным теоретическим выкладкам в работе  http://fatyf.narod.ru/cinema.htm

 

Значит, есть у нас два велосипедиста. Один стоит на старте, второй в десяти метрах перед стартом. Сначала второй велосипедист разгоняется со своей позиции так, что в момент времени t=0 он проезжает мимо первого велосипедиста со скоростью 10м/с. С этого момента начинаем наш эксперимент.
В момент времени t=0 первый велосипедист начинает разгоняться с ускорением 1м/с/с, второй к этому моменту уже набрал скорость 10м/с и далее двигается равномерно. На протяжении последующих 10 секунд, вплоть до момента t=10 скорость первого велосипедиста меньше скорость второго велосипедиста. И только в момент t=10 скорости обоих велосипедистов станут равны 10м/с.
Итак. в течении 10 секунд первый велосипедист ехал все время медленнее второго. Казалось бы, отсюда однозначно следует, что второй велосипедист за эти 10 секунд проехал большее расстояние, чем первый. Но у нас есть формула премудрого Александра Фатьянова, которая говорит, что пройденный путь зависит исключительно от скорости в конце пути, а значит оба велосипедиста проедут одно и то же расстояние за одни и те же 10 секунд, хотя один все время движется быстрее второго....

Ответ:

к моменту t0 Второй уже проедет 10 метров, а первый стоит. Пока второй равномерно едет, первый разгоняется и расстояние растет и к моменту когда первый достигнет скорости второго, тот будет двигаться не 10, а 11 секунд и находится в 110 метрах от точки своего старта. Но расстояние между ними станет 10 метров. Первый догоняет второго на ту же разницу что и при старте. Та же десятка метров и останется. но останутся и проделанные 100 метров первым.

 Позднее примечание:    тут вкралась ошибка,  первый достигнет скорости второго гораздо раньше,  уже на промежутке между пятой и шестой секундами, и дальше будет еще разгонятся!!!!! Что не мешает ему  принципиально обогнать после десятой, уже на одиннадцатой секунде движения!!!!.

То есть статус кво достигается на 10 секунде,  только и всего!!!!

Расстояния, пройденные разгоняющимся велосипедистом, и тем который проезжает мимо него без ускорения  при одинаковом времени совместного движения будут именно одинаковыми, при условии, что время разгона первого и равномерного движения второго одинаково.

Немного не так. Ниже приведена более точная формулировка.

Какую  бы временную фору t  не имел бы  ранее стартующий, и двигающийся после этого равномерно спортсмен, он,  в конце концов, останется позади стартующего позже, но двигающегося то же время с ускорением.

 

 

 

Путь у первого вычисляется по формуле s=v0t+at2

 

Что мы и наблюдаем на стадионе.

Даже если совершен фальстарт, стартующие позже никогда не окажутся далеко позади стартовавших раньше, расстояние к моменту разгона отставших сокращается за время ровно такое сколько потребовалось чтоб убежать первому, при одинаковой, допущение, подготовке спортсменов.

А по сегодняшней кинематике:

Путь второго велосипедиста составит 50 метров. По формуле  s=v0t+at2/2

Путь первого от момента времени t0   составит  100  метров.

 Таким образом, отставание первого от второго на момент t10 составит 60 метров с учетом разницы при старте. Что не подтверждается опытом.

 

Оппонент забыл, что по любой из формул пройденный путь квадратично зависит от времени. График этой зависимости является параболой. Следовательно, расстояние между велосипедистами только сначала растет, но потом сокращается согласно этой зависимости.

То есть и однозначный вывод. Без всякого казалось бы.  Ускоренное движение на второй половине пути быстрее равномерного.

 

Еще и вопрос, а как и с каким ускорением разгонялся первый велосипедист, имеющий фору в одну секунду. Он должен был за одну секунду ускориться до 10 м/сек.

То есть ехать с ускорением 20.  по формуле s=at^2/2,    a=2s/t^2

 

 

 

Далее пишем расчеты.

 

По классической формуле   с места.    S=at^2/2

     начальные условия

  t=1 сек,  s=10 метров 

получим   a=2s/2=20,

но

 по известной формуле V=at = 20 метров/сек  и никак не 10 -- начало равномерного движения из условий задачи.

Что не соответствует начальным условиям.

Но это просто как уточнение.

 

смотрим, как это делается по-нормальному, если следовать канонам высшей математики:

 

v=ds/dt  a=dv/dt=d²s/dt²  в дифференциальном выражении

 

интеграл от скорости равен пути,   интеграл от ускорения равен скорости.

интеграл скорости---сумма отрезков пути, отнесенная к времени и берется по времени,

 

подинтегральное выражение  s/t dt

 

интеграл от ускорения ---сумма скоростей на этих отрезках, отнесенная к времени , берется

по времени.

Подынтегральное выражение   s/t2 dt    ( для справки:  интеграл от функции 1/x^2  dx=1/dx  по абсолютной величине, т к. скорость не бывает отрицательной)

 

время движения разбивается на одинаковые интервалы dt =1 сек

на первом интервале  скорость V численно равна ускорению

 

  пройденный путь на любой секунде (общий путь) S=at^2

расчет интервала пути: Si+1=S-Si , где  i-  номер интервала времени

расчет скорости на интервале  времени Vi=(Si+1)/dt

скорость на всем пути за количество секунд на данное время (общая)=сумма скоростей на отдельных временных интервалах.

расчет делается  для ускорения a=1 м/сек^2

 

секунды                                1    2    3     4       5      6      7      8     9     10

общий путь  S                       1    4     9   16      25    36    49    64   81    100

интервал   пути    Si               1    3     5   7        9      11    13    15   17    19

ds-разность путей Si-Si-1             2     2    2       2      2       2     2      2     2

скорость на интервале

времени dt---- Vi                   1     3     5    7      9      11     13    15   17    19

скорость общая   V               1    4     5   16     25     36    49     64   81    100   (метров за n секунд)

 

теперь  проверим на любом из интервалов ускорение

a=(v4-v3)/t ,    Поскольку скоростей две, значит и количество интервалов времени равно 2.

a=(7-5)/2=1   что и требовалось получить. Для первого интервала скорость численно равна ускорению.  

Заметим, что разность скоростей и разность путей для каждой пары интервалов является величиной постоянной,  как и ускорение, что и определяет равноускоренное движение с постоянным ускорением.

 

 

А  скорость физически не  может быть отрицательной по одной простой причине, она не может быть меньше нуля при прямолинейном движении в одну сторону. Направление движения  не меняется. Графики является геометрическим представлением зависимости  скорости от времени  при  Равноускоренном и Равнозамедленном движении, если быть точным.  Знак минус у скорости является признаком равноускоренного движения. А знак плюс признаком равнозамедленного. И не более того.  Условность.

 

Интегральное «доказательство»  рассмотрим в следующей статье.  Хотя в этом особой необходимости и нет. 

 

Интегральное доказательство именно из учебника.

v=at  а-сonst.

Известно, что v=ds/dt --> надо найти функцию s=s(t), производная которая равна at. Результат at2/2, простенько и со вкусом, забывается про обязательную последовательность операций дифференцирования и обратную последовательность операций интегрирования.

v=ds/dt

a=d²s/dt²

a является результатом дифференцирования дважды пути по времени.

 

Это   принцип дифференцирования предложен не кем иным, как самим Ньютоном в «Началах»

И операция обратная дифференцированию-интегрирование осуществляется в точном обратном порядке.

Интеграл от ускорения – скорость,  интеграл от скорости путь.

 в формуле v=at произведена алгебраическая замена оператора дифференцирования, и ускорение перестало быть Функцией скорости от времени и стало константой-цифрой, величиной неинтегрируемой.

Что и проявляется при Анализе Неравноускоренного движения!!!!

там этого пропадания не будет.

Обратная операция интегрирования данного выражения предполагает вынос постоянной за знак интеграла, а значит игнорирование вообще ускорения как величины физической.

Под знаком интеграла остается tdt и интегрируется только время по всем правилам табличного интегрирования вместо интегрирования второй производной a=d2s/dt2

результат такого "доказательства" укорочение расстояния вдвое по расчетной формуле.

ДАННОЕ ДОКАЗАТЕЛЬСТВО НЕ ПОДТВЕРЖДАЕТСЯ ОПЫТОМ!!!!

 

 

http://my.mail.ru/community/vartan/392F75A7FC67B6A0.html?skip=0

 

 

Дополнение.

Представленные доказательства вполне объясняют, почему звук от якобы летящего со сверхзвуковой скоростью снаряда опережает происходящий рядом взрыв.  Расчетная начальная скорость снаряда завышена вдвое.

 

 

 

Фатьянов А.В.   Спб.   1.02.2011  правка от 9.09.2011---включены расчеты и исправлены  несущественные ошибки.