Вопросы по механике Ньютона, и ответ на одну современную публикацию.

Основной вывод. Мы не правильно понимали до сих пор понятие кинетической энергии. mv²/2. Мы имеем двойную бухгалтерию и присутствие черного нала в кассе физики. Это двойной учет перемещения, представленный квадратом скорости.

Как-то совсем неожиданно всплыла из моего архива старая статья { ТОЧНОЕ ЕСТЕСТВОЗНАНИЕ – ОСНОВА МИРОПОНИМАНИЯ

Смирнов А.П. Международный клуб ученых. Санкт-Петербург. Россия. }

(http://fatyf.narod.ru/smirnov20042.htm

прошу заранее извинить автора за несанкционированное копирование), посвященная критике современной трактовки законов Ньютона.

Само название привлекло.

К сожалению прямой ссылки сегодня обнаружить не удалось, зато есть ссылка на платное пользование его книги: http://www.shaping.ru/mku/smir16.asp

Где приведен прекрасный обзор тем, представленных там автором.

Не знаю, является ли автор профессиональным физиком, но вопросы механики поднятые им стали достаточно плотно пересекаться с моим собственным мнением о механике …

Итак.

P=mv импульс,

F=ma сила

Ньютон, понятно.

E=mv²/2 кинетическая энергия

Творение Кориолиса.

Независимо от Ж. Понселе он ввел в 1826 в механику понятие «работа» и, исходя из него, сформулировал теорему «живых» сил. Причем за меру «живой» силы принял половину произведения массы на квадрат скорости.

Работа:

A=Fs cos a

«С утверждением паровой машины в промышленности и с разработкой ее полной теории в мир науки полноправно вошли новые понятия — работа и энергия, понимавшиеся уже практически с современных позиций. Например, французский ученый Жан Виктор Понселе говорил об этом так:

«Исполнять работу в техническом смысле слова — это значит преодолевать или уничтожать сопротивление. Механическая работа — это постоянное преодоление сопротивлений силой, действующей вдоль пути и в направлении этого пути».»

Третий закон Ньютона F₁=-F₂

_{Тела попарно действуют друг на друга с силами, имеющими
одинаковую природу, направленными вдоль прямой, соединяющей центры масс этих
тел (абсолютно-твердые тела), равными по модулю и противоположными по
направлению.}

От автора статьи:

«По существу, это было уже то определение работы, которое позволило другому французскому ученому Л. Навье ввести в 1826 г. классическую единицу работы — килограммометр.»

Ньютон в своих «Началах» о работе и энергии даже не упоминал. Не видел, скорее всего, смысла.

А единица классической работы не килограммометр вовсе (как без секунды в квадрате?).

Именно эти четыре формулы на сегодняшний день определяют аксиоматику динамики в механике.

Вопрос нулевой.

Чем отличается работа от кинетической энергии. Fs cos a от mv²/2 ?

cos a

а что смущает?

1/2 и наличие квадрата скорости V²

Cos a первая неясность в классической физике, поскольку она, как правило, не видит разницы между работой и кинетической энергией.

Посмотрим, как это делается в школьном курсе

При равноускоренном движении перемещение s выражается формулой s=(v₂²-v₁²)/2a

Отсюда следует, что A=Fs=ma(v₂²-v₁²)/2a=mv₂²/2-mv₁²/2

Это выражение показывает, что работа, совершенная силой (или равнодействующей всех сил), связана с изменением квадрата скорости (а не самой скорости).

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

E=mv²/2

Работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии. A = E_k2 – Е_k1.

Это утверждение называют теоремой о кинетической энергии. Теорема о кинетической энергии справедлива и в общем случае, когда тело движется под действием изменяющейся силы, направление которой не совпадает с направлением перемещения.

Очень ловко, однако. Взять из кинематики (равноускоренное движение) начальную и конечную скорости. Посчитать по формуле путь и подставить в выражение силы совершенно чужую математику.

Все дело в том, что в такой формуле из кинематики не рассматривается начало движения с места.

Во-первых, ускорение рассчитывается из имеющейся уже скорости a=(v₂-v₁)/t

и при v₁=0 a=v₂/t это по определению самого ускорения. При этом размерность ускорения м/сек2.

То есть ускорение при движении с места численно равно скорости на конце отрезка S.

А при формуле из кинематики s=v₀t+at² /2 подстановка v₀=0 (v=s/t, a=s/t²) даст только половину пути. S=s/2

Проверка подстановкой!

Формула s=v₀t+at²

Дает верный результат! То есть, при нулевой начальной скорости и тех же подстановках условие равенства выполняется, путь останется путем.

Из «школьной кинематики» имеем

s=(v₂²-v₁²)/2a

или a=(v₂²-v₁²)/2s при 0-й начальной скорости v₁=0, ускорение а=v₂²/2s

м²/2м сек²

подставим v²=(s/t)²/2s a= (s/t²)/2 При сокращении размерность такая же, м/сек2, но!!!!!!

Появляется злосчастная половинка (1/2) и вдвое меньше путь!

Откуда??????

«При анализе равноускоренного движения иногда возникает задача определения перемещения тела по заданным значениям начальной υ₀ и конечной υ скоростей и ускорения a. Эта задача может быть решена с помощью уравнений (υ = υ₀ + at.) и (S=V₀t+at²/2)путем исключения из них времени t. Результат записывается в виде

S=(V²-V₀²)/2a

Непонятно, как связать эти два уравнения человеку не знающему математического анализа, с его интегралами да дифференциалами. Да и там, как оказывается, все средства хороши.

Его просто ставят перед фактом. Время убрали и получили. А то, что при подстановке нет равенства, так и сами не видим!!!!!! даже не задумываемся почему.

Оказывается, что путь в школьной кинематике определяется еще графически!!!! По графику зависимости скорости от времени. v/s

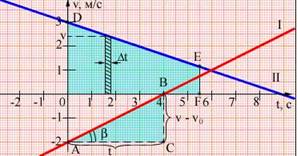
«График скорости позволяет также определить проекцию перемещения s тела за некоторое время t. Выделим на оси времени некоторый малый промежуток времени Δt. Если этот промежуток времени достаточно мал, то и изменение скорости за этот промежуток невелико, т. е. движение в течение этого промежутка времени можно считать равномерным с некоторой средней скоростью, которая равна мгновенной скорости υ тела в середине промежутка Δt. Следовательно, перемещение Δs за время Δt будет равно Δs = υΔt. Это перемещение равно площади заштрихованной на рис. 1.4.2 полоски. Разбив промежуток времени от 0 до некоторого момента t на малые промежутки Δt, можно получить, что перемещение s за заданное время t при равноускоренном прямолинейном движении равно площади трапеции ODEF. Соответствующие построения выполнены на рис. для графика II. Время t принято равным 5,5 с.

S=(OD+EF) OF/2 = (v₀+v)t/2=(2v₀+(v+v₀))t/2

Попробуем (без геометрии) подставить начальную скорость v₀=0

S=v t /2, подставим v=s/t, и путь автоматически уменьшился вдвое. Скорость то считаем по среднему!!!!!! А разве можно брать среднее от и так бесконечно малой величины?

Какая может быть проекция при v=s/t как функции от t, если прямая является геометрическим местом точек значения ускорения? Оно на всей прямой определяет скорость перемещения в определенный момент времени. Ускорение одно, движение равноускоренное. Угол наклона прямой связан с ускорением

а=tgb=(v₂-v₁)/t определение ускорения!!!!

И этот угол постоянен!!!!!

Задавая отрезок на такой прямой мы имеем проекцию на ось времени (а-a)cosa= t₂-t₁.

И такую же по смыслу проекцию на ось скорости. Какая площадь????

Зато из любой точки на гипотенузе треугольника АВС можно опустить перпендикуляр на катет и получить сколь угодное число подобных треугольников, для которых а=tgb=const что и означает их математическое значение!!!!!!

Функционально f=(v/t)/t=s/t²=a где v=s/t

Вычисление пути s=(v₂-v₁)*(t₂-t₁) ни к графику, а тем более к площади трапеции не имеет никакого отношения.

Остальных аспектов такой «математической физики» можно и не рассматривать.

А задача поиска уравнения движения решается без особых трудностей.

http://fatyf.narod.ru/cinema.htm

Откуда хочешь взять формулу, оттуда и бери!!!! Любую, кроме, верной.

Если использовать формулы a=(v-v₀)/t и s=v₀t+at²

А именно их и надо считать математически верными, получим исчезновение 1/2.

И отсутствие необходимости искусственного введения квадрата скорости.

То есть A= Fs cos a , Е = mv²/2 является недоказанной, к тому же классика теряет при своих экзерцициях сам угол…. Спрятав его за мало заметной фразой, сила…,направление которой не совпадает с направлением перемещения. Что уже интересно не только с математической точки зрения.

Вывод.

В кинематике неверно просчитывается перемещение материальной точки. Введение средней скорости на бесконечно малом отрезке в условии равномерности движения приводит к занижающей оценке длины перемещения.

Это с математической точки зрения…..

С точки зрения обывателя: Едем на машине и видим впереди другой автомобиль, соблюдаем дистанцию. Вдруг первый начинает тормозить, а мы тоже тормозим и, бац в ему по бамперу и подфарникам. Авария. Приезжает инспектор, измеряет тормозной путь, сверяет по таблицам такой «кинематики» и Мы ВИНОВАТЫ!!!!

При доказательстве не использовано прямое(без квадратов скоростей) определение ускорения, а значит доказательство явно натянуто.

.Вопрос 0, ответ: Разница не устранена. А сам вывод mv²/2 явно ошибочен..

Далее рассмотрим все более углубленно.

Вопрос первый.

Кинематика, благодаря Лейбницу и Ньютону, которые ввели дифференциальное и интегральное исчисление, выражает через дифференциалы значения скорости и ускорения следующим образом:

v=ds/dt

a=dv/dt=d²s/dt² Где s – перемещение, t-время.

Динамика Ньютона подразумевает те же операции при наличии массы.

P=mv =m ds/dt импульс,

F=ma =m dv/dt= m d²s/dt² сила

В данных формулах само перемещение уже учтено. Можно взять и третью производную от перемещения по времени. Однако к энергии и работе отношения это иметь не будет. Скорость изменения скорости. Оно нам надо? Только для анализа неравноускоренного движения.

Умножение силы на перемещение A=Fs при определении понятия Работы означает масло масляное, поскольку дважды учитывать одно и то же физическое изменение состояния попросту казус, если по-честному - абсурд.

Полное непонимание процесса.

А почитав статью, (где черным по белому приводятся цитаты из Ньютоновых «Начал» и полистав для очистки совести и саму монографию Ньютона) где автор еще и силу умножает не просто на перемещение? а на скорость (FV) , я наконец-то обнаружил предмет личных сомнений и совсем неладное в современной трактовке и работы и кинетической энергии. Складывается такое чувство, что у читающих и использующих данную формулу определения работы с математикой совсем плохо, а то и там и там. Такое же встречается и у Фейнмана.

А Ньютон не зря ввел понятие дифференциала при определении силы. Не зря не затронул и понятия энергии и работы. Сила уже является фактом движения, так как есть скорость и ускорение, есть и ежу понятный путь, на котором они вычисляются, то есть действие уже сделано!!!. РАБОТА сделана. Она и есть то самое искомое физическое, материальное, перемещение массы в определенном направлении. То есть в силу входят в необходимом и достаточном количестве все исходные данные (энергетические составляющие) перемещения массы на требуемое расстояние в заданное время. Таким образом, учитывается и прямолинейная траектория этого движения.

И третий закон лишь констатирует различие направлений этих ускоренных движений.

m₁a₁=- m₂a₂

если тела отталкиваются друг от друга при взаимодействии за счет внутренней энергии(накопленного импульса). Типичное отталкивание от опоры при ходьбе.

А если быть совсем точным, то эта формула(с абсолютными по величине силами

F1=F2) является условием отсутствия движения. Состояние достигнутого равновесия. Закон сохранения равновесия. Закон рычага. Если больше или меньше, движение продолжается: большее движет меньшее.

Импульс или количество движения P=mds/dt по сути своей физической есть Энергетическая единица действия (количество движения) в дифференциальной форме и является мерой энергии процесса. Сила это уже кинетическая энергия движущейся массы независимо от времени действия для процесса перемещения эта величина постоянна. И тогда в качестве потенциальной (внутренней) энергии выступает сама масса.

Импульс есть интеграл от силы.

Эти две характеристики движения неотрывно связаны друг с другом, одна характеризует зависимое от времени значение энергетики процесса, вторая растянутость процесса во времени. И никакие другие характеристики для описания движения тела в точечном представлении не нужны.

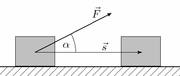
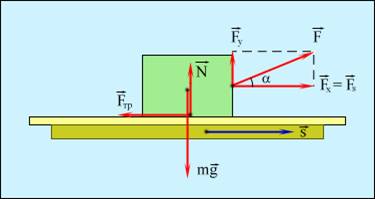
В учебниках рисуют подобные картинки и даже представляют нам, что работа есть проекция силы на перемещение…, которое и так уже есть.

Факт то, что Сила действует постоянно, пока мы перемещаем тело. Чтобы сдвинуть тело, надо преодолеть силу трения и силу упругости самого тела. Сдвинув тело целиком, мы имеем право говорить, что для данного перемещения с полученным ускорением была уже применена сила эквивалентная массе тела с указанным ускорением.

Вопрос: что же такое сила, если нам надо ее превратить в энергию, из каких параметров мы определяем силу? Массы, времени и перемещении этой массы. Из пройденного пути за время. Скорости и ускорения. То есть в исходных данных уже заложен путь, задано время движения массы тела. Получается, что векторное изображение силы сам процесс игнорирует и заставляет осуществить его еще раз.

И что мы делаем, когда используем исходные данные повторно. Мы делаем двойную регистрацию перемещения.

Как надо изображать? Раз сила действует постоянно, она не может быть единичным вектором, это множество условных векторов. Можно изобразить вектор скорости и ускорения, но вектор, умноженный на массу уже не математический вектор. Это физическая величина и обращаться с ней надо очень осторожно. Волюнтаризма она не терпит. Масса всегда имеет размеры, определенные свойства и чисто математические операции с массой не являются отражением физического процесса с ней происходящего. Масса это не математическая точка. Подобные упрощения годились на заре становления науки и уже неприемлемы в настоящее время.

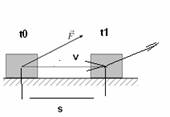
Например, в начальный момент сила может быть и приложена, но недостаточная для начала движения тела целиком. Действуют сила трения и сила упругости. Компенсация этих сил есть условие для начала движения. Движение до того происходит внутри самого тела. А угол приложения силы лишь изменение пропорций действия этих сил внутри тела.

Что такое работа? Работа это результат. Констатация Факта перемещения. Как можно описать работу энергетически – никак. Только словами. При затрате какой то силы произведено перемещение. Процесс работы это процесс расходования силы. То есть и энергии по частям. А по формуле mv²/2 получается, что энергии затрачивается больше чем силы.

Откуда половинка в классической энергии? Чтоб проинтегрировать и получить силу. И это не Изобретение Ньютона. Повторимся, зря человек не придумал бы дифференциальное и интегральное исчисление. И не стал бы его путать с обычной арифметикой. А тем более с векторной алгеброй, которой в настоящее время пытаются доказать справедливость mv²/2

Выдержка из официальной трактовки кинетической энергии. ( википедия)

Рассмотрим систему, состоящую из одной частицы, и запишем уравнение движения:

$m \vec a = \vec F$

$\vec{F}$ — есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы ${\rm d} \vec s = \vec v {\rm d}t$ ???????????????? ds ds/dt²????????. Учитывая, что $\vec a = \frac{{\rm d}\vec{v}}{{\rm d}t}$ , Получим: (а не получается однако без подгона и умножения на 1/2).

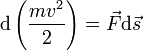
${\rm d} \left( {{m v^2} \over {2}} \right) = \vec F {\rm d} \vec s$

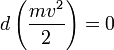Если система замкнута, то есть $\vec F = 0$ , то $d \left( {{m v^2} \over {2}} \right) = 0$ , а величина

$T = {{m v^2} \over 2}$

В результате мы интегрируем неизвестно что с физической точки зрения, но в результате получаем силу, с заранее подготовленным планом интегрирования по общепринятым правилам. Вот откуда ½ ПОЛОВИНКА !!!!!! ниоткуда!!!!

Если брать третью производную по времени от перемещения получим ненужный нам результат. Но такой же нонсенс получается и при умножении силы на расстояние. Поскольку само расстояние уже учтено в ускорении и скорости. Все уже есть в производных.

Сама физика заставляет в отношении основных понятий остановиться на Работе и энергии, как синониме количества совершенного движения и понятии импульса, то есть о действии на малом промежутке, а на силе как мощности. То есть не мгновенной затраты энергии, а необходимой постоянной энергии в предположении противодействующих сил..

Что можно использовать для коротких процессов и для протяженных в одинаковой мере.

В чем разница от современного представления. Импульс есть выражение энергии на коротком не меняющем направления перемещении, mv, сила есть постоянно прилагаемая мощность для поддержания движения по траектории с учетом противодействия.

Автор в представленной статье приводит высказывания Ньютона на эту тему и тут же вводит понятие креатона, что тут же и таким же образом, только еще хуже наводит так им раскритикованный хаос. Порядок должен быть. Не только на словах, но и на деле. На то и бухгалтерия. А то так еще одна петрушка смешная с причинителем движения.

Какой смысл введения второй раз скорости, если она учтена в силе. Это допускает и еще повторного введения, и еще, что доводит дело до абсурда. С таким же успехом можно и импульс домножить на перемещение. Только что от этого выиграет физика?

Да ничего кроме головной боли.

Это касается вращательного движения и момента импульса.

Некоторые защитники формулы mv²/2 применяют и другие запрещенные приемы. Например: называют эту формулу градиентом силы. То есть?

Есть Определение градиента. Производная функции по данному направлению равна произведению градиента функции на единичный вектор направления.

Единичный вектор направления не имеет переменного численного значения…. Это орт. Длина такого вектора равна 1 (единице)

dF/ds= m/t² получили не весть что физически. Это не градиент, а бог знает что.

Градиентом может быть, например: изменение плотности dp/ds=grad p S где плотность измеряется в кг/м³, то есть имеет смысл говорить о направлении в трехмерной системе координат. В нашем случае этого нет. Система координат имеет всего лишь одну координату по длине, а следовательно, и одно единственное направление.

Но еще в данном случае сила уже вектор, и само перемещение, входящее в силу тоже вектор, а перемножение двух одинаковых векторов перемещения, а тем более двух одинаковых направлений в векторной алгебре может и позволительно, но физически смешно. Так же это относится и к перемножению одинаковых векторов скорости. Такое перемножение может имеет физический смысл, когда между векторами имеется угол, хотя и это проблематично. Складывать куда ни шло, а вот, например две скорости перемножить даже в разных направлениях уже вопрос, есть ли в этом здравый и физический смысл?

И еще одно. Никак дифференцируя путь по времени не получить величины ½. А и тут потеряли косинус!!! Да не просто потеряли, а посеяли недоверие.

Если мы под углом к силе тяжести прикладываем к телу силу, значит, приподнимаем тело и уменьшаем его вес. То есть, уменьшая в общем действие сил трения, заставляем больше работать силы упругости в частности на изгиб.

А поскольку в векторной алгебре подобной операции с одинаковыми векторами и направлениями, все-таки, не обнаруживается при тщательном рассмотрении, ошибку маскируют перемножением вектора силы на скаляр. Но от этого скалярное значение уже учтенного перемещения не пропадает. Путь даже не просто складывается, а умножается.

В заключение необходимо отметить, что при рассмотрении двух формул ma и mv²/2 и численной подстановке пути и времени, выясняется, v²/2 растет быстрее ускорения, энергия растет нелинейно и быстрее самой силы, что возможно и явилось поводом спекулировать этой разницей, то есть на явной ошибке построить целую теорию. Кстати, рост явно по показательной функции, если не экспонента.

Импульс вполне необходимое и достаточное количество движения для определения закона сохранения энергии..... не имеет смысла вводить два пути, делить это туда-обратное или двойное движение на количество ходок....

По идее получается, что сила отражает динамику передачи энергии от одного ее потенциала к другому. А импульс отражает зависимое от времени действия силы значение этой энергии.

Равновесие сил означает равенство потенциалов энергии в различных точках пространства. Что и выражает третий закон Ньютона, записанный в дифференциальной форме как закон равенства импульсов.

mv=-mv

Вопрос второй.

Почему для одного объекта, имеющего массу и форму (геометрические размеры), площадь приложения силы, мы должны опускать два этих немаловажных последних и определяющих механическое взаимодействие фактора и сводить все до точки?

Правда это можно рассмотреть и в другом месте, хотя хотелось бы знать: вообще кто-либо задумывался ли над этим? Выяснилось, задумываются:

http://newrotor.narod.ru/low.html#76

да и в механике есть уже два определения.

Одно из них называется давлением.

P=F/s

Второе получается из закона Гука при растяжении стержня:

отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением.

И единственно на что поры пока не ссылаются на прямую учебники, это колебательные процессы внутри тела при ускоренном движении под действием силы. Проблемы эти возникли впервые в самолетостроении и в частности послужили основанием для работ Келдыша по борьбе с так называемым флаттером.

Есть такое понятие как момент силы.

М=Fs

И есть архимедов рычаг и правило равновесия рычага.

F₁D₁=F₂D₂

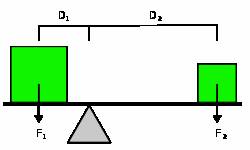
Какое замечательное совпадение с вышеприведенными высказываниями.

Вот она «еще одна работа», не производимая никакими силами - момент силы. М=Fs

Одинаковость формул.

Правило Архимеда.

Проигрываем в расстоянии – выигрываем в силе.

Вот физический смысл классической «РАБОТЫ и ЭНЕРГИИ» одна и та же математика. Но вот тут действительно сила умножается на скаляр длины рычага к перемещению не имеющего никакого отношения.

И нечего больше на Эйнштейна пенять коли и у самих физиономия в пушку. Не он первый начал, он продолжатель традиции не ньютоновой и не архимедовой кривой в принципе механики, приведшей к кривизне пространства-времени.

Получается из этого правила, что в понятии энергии нет никакого смысла, оно и заключено в двух производных от перемещения массы по времени, то есть в импульсе и силе. И естественный вывод, чтобы изменить что-то численно в этом правиле, необходимо менять либо массу, либо ускорение, либо длину рычага и нарушать равновесие. Никаких лишних скоростей и половинок.

Архимед в действии.

Но это при точечном представлении массы. Площадями и изгибами занимается сопромат.

Возникает вопрос. Производятся ли затраты энергии при равновесном положении рычага? Конечно, нет. Скорее всего, именно так ответит классическая физика. Так как нет движения.

3-й Закон Ньютона опровергает такой вывод напрочь. На силы Мg действует сила реакции опоры. Это сам рычаг с его упругостью и упругая опора. Поэтому происходит взаимный обмен энергией, в равных количествах черпаемой из внутренней энергии упругости всех тел. Под опорой понимается естественно земля. А это означает и взаимо-действие, взаимное движение. Есть силы, значит, движение имеем. Вопрос только какое, но это уже объяснить именно механикой не получится.

А производятся ли затраты энергии если в равновесном положении на одно из плечей положить груз, таким образом нарушив равновесие. И что это за энергия.

Если для свободного падения тела есть формула потенциальной энергии E=mgh, и

Работа вычисляется как :

A = –(Eр2 – Eр1). Разница потенциальных энергий в начале и конце пути , то для несвободного необходим расчет.

Классическая формула сразу ответ не даст. Поскольку неизвестен путь, по которому начнет двигаться конец рычага. Придется сначала рассчитывать траекторию движения, учитывая силу трения, силу упругости рычага. Составлять уравнение движения несвободного падения тела. Принять в учет и колебательную составляющую процесса. Плюс уравнение равновесия самого рычага.

Ответ c с позиции Ньютона очевиден. А=Е=mg со стороны добавленного веса больше ничего и не требуется. Все остальное это уже результат. И определение траектории движения, скорости и пути. Была бы приложена постоянно действующая сила, и силы сопротивления движению.

Более качественно закон сохранения энергии звучит как закон сохранения импульса. Скорость совершенного передвижения массы равна скорости совершенного противодействия на прямолинейном участке. Тогда в силовом или мощностном выражении сила совершенного действия равна силе оказанного противодействия.

А нынешнее понимание законов ньютона предполагает расчет сил из несуществующего действия. То есть mg=-kx тело лежит на опоре, опора сопротивляется. Но ведь это чистая условность в предположении макроскопичности тела и присутствии уже совершившейся деформации опоры. При этом деформация самого тела не рассматривается. Мы это называем весом тела. Не менее не более чем условно!!!! Вес тела измеряется в ньютонах, масса в килограммах. Но вес мы принимаем за массу и приблизительно 10 ньютонов оцениваем как килограмм.

Таким образом, потенциальная энергия тела поднятого на любую высоту физического смысла не имеет. Она заключена в самой массе и вычисляется сегодня условно опять же исходя из ускорения свободного падения меняющегося с высотой и двойного учета самой этой высоты. На самом деле это кинетическая энергия условно упавшего тела. А теперь пример из жизни. Каковы потенциальные энергии падающих камня и гранаты, которая падает и может во время падения взорваться? Ответ кроется в отождествлении внутренней энергии и потенциальной энергии в выражении массы и свойств вещества, из которого она состоит. В этом принцип вложенности или рекурсии. Что-то новое надо вычислять из известного старого. Любая сила есть действие других составляющих ее сил. А масса – единственный пока способ их измерения на основании веса. То есть сравнения.

Вопрос третий.

Как нам быть с гипотетической силой инерции. Да никак. Ньютон вообще упомянул инерцию в трех своих томах один раз. Раз в последствии введена фиктивная сила, то просто ее надо раскрыть в том же ключе философии физики Исаака Ньютона. И направлена она будет по направлению движения навстречу силе сопротивления.

Все дело в том, что механика Ньютона занимается движением макроскопических тел и не рассматривает никаких процессов внутри самих тел. Она не занимается ни трением ( тот замечательный COSинус в работе как раз уменьшение силы трения и учитывает), ни упругостью. Она не учитывает действия этих сил возникающих в процессе страгивания тела с места. Именно поэтому так четко и выдан первый закон Ньютона. На внутренние силы (энергетику) законы Ньютона распространяются, как на систему малых тел и не могут быть поломаны, без серьезнейших на то причин простыми математическими фокусами и манипуляциями физическими величинами.

Попросту инерция есть свойство любых физических тел имеющих массу накапливать внутреннюю энергию в процессе начала видимого движения (более или менее просто регистрируемого факта). Накопление сил, по-русски!!!! И свойство тел ее расходовать, уставать, по-русски!!! Аккумуляция энергии и расход энергии в процессе движения.

Что такое мера инерции – это масса? Масса, при одном условии, при движении масса не увеличивается за счет других масс. И не уменьшается за счет реактивного движения. Пришлось немного поразмышлять и результат - стыковка Ньютона с законом Гука. См. (6 вопрос).

Инерция или сила упругости воплощается в Законе Архимеда, используемого в физике, в частности в гидростатике. Это уменьшение плотности (расширение, или изменение формы) при уменьшении внешнего давления и наоборот. Этот закон действует для всех тел независимо от их агрегатного состояния. То есть распространяется и на сами атомы.

Чем больше скорость, набранная в начале (движение с ускорением), чтоб потом уже превратиться прямолинейное равномерное движение, тем больше действие сил упругости заключенных в самой массе. В процессе движения, если на тело ничего не действует, действуют именно эти силы.

В конечном итоге, сдвигая тело из состояния покоя, (в отсутствии внешних сил трения) начиная от места приложения силы на тело в целом и на его атомы оказывается растягивающее(или сжимающее) действие, неравномерно меняется плотность, в результате чего каждая мельчайшая частичка приобретает импульс, направленный в сторону движения. Этот суммарный импульс и двигает тело в отсутствие действия сдвигающей силы. То же и с силой толкающей- тогда сжатие.

Что происходит в самом теле во время движения, когда пропадает двигающая внешняя сила?

Начинают работать силы упругости, и внутри тела начинается затухающий колебательный процесс, сжатие и расширение, поскольку первоначальное сжатие или расширение производится неравномерно по всему телу и не мгновенно.

Каждый атом тела, система упругая и вращающаяся, следовательно, при любой деформации изменяется скорость вращения, а со скоростью и размеры, перераспределение внутриатомной плотности. Гироскоп.

Каждый атом тела сталкивается с атомами среды, столкновение обязательно ведет к обмену импульсами, их перераспределению внутри тела. Внутри все время при обмене внешними ударами идет колебательный процесс перераспределение давления и плотности.

Если сопротивление среды отсутствует, обмена импульсами нет и нет расходования энергии. То есть сжатое тело ее сохраняет и плотность не падает, никуда не пропадает энергия, запасенная вращением. Вроде как парадокс. Внешне имеется кажущееся быстрое восстановление размеров, но чисто внешне. На самом деле при полном отсутствии внешних сил закрученные гироскопы атомов только расширяют это тело до бесконечности, до полной их остановки.

Закон Архимеда – уменьшение плотности при уменьшении давления.

Следовательно, есть силы, помимо известных сил, механических, которые не дают телу расширяться до бесконечности.

Именно в такой постановке действия сил упругости достаточно просто объясняется эффект Джанибекова.

См. http://intelogic.ru/news/perevorot_zemli_ehffekt_dzhanibekova/2010-10-02-47

Переворачивает сила упругости (инерции),

происходит перемещение центра масс из-за колебательных процессов внутри вращающегося тела, постоянное перераспределение плотности, а отсюда и перемещение центра масс. И никаких полей рядом не стоит. А квантованность процесса переворота объясняется тем, что напряжения деформации накапливаются медленно, а срабатывают скачкообразно, катастрофа.

Подобный эффект работает и при сваливании самолета в штопор.

Этим эффектом объясняется и прецессия волчка, замечу, она в конце при малой скорости вращения и делает заметные колебания-Нутацию. http://ru.wikipedia.org/wiki/Нутация

Достаточно сильно данный эффект должен работать при полете бумеранга.

Совместно с эффектом Магнуса и подъемной силой.

В космосе несколько другая ситуация.

Вопрос... Если это будет в присутствии воздуха на космической станции и отсутствии веса, траектория полета естественно изменится. Считать надо и нужно математику с учетом всех эффектов. Вполне вероятно подъемная сила ведет там по-другому, нежели на земле. Кто там пускал самолетик???? Эффект Магнуса должен работать, и эффект Джанибекова без серьезных поправок.

Вывод для станции: скорее да, чем нет и достаточно быстро бумеранг должен вернуться, но траектория полета будет иная, чем на земле.

Второй вариант это безвоздушное пространство. Первые два эффекта пропадут, третий будет зависеть от сопротивления среды, чем меньше тем дольше период переворотов. среда как не крути, хоть какая-то, имеется. Это вещество и всевозможные излучения на всем спектре частот.

Вывод для космического вакуума: возможно вернется, но очень не скоро и не обязательно абсолютно точно. Следует на крайне больших расстояниях принимать в учет как разновидность эффекта Магнуса – Эффект Садовского.

Вопрос четвертый.

Касается работы и энергии во вращательном движении, в том числе и рычага, если излагать предмет с таких же позиций. Частность, которую при данной постановке вопроса можно решить в последующем.

Дополнение от 22.10.2010

Безотлагательно надо возразить только против «момента инерции» и

«момента импульса», придуманного, по-видимому, в угоду квантовой механике и теории относительности.

Рассмотрим момент инерции.

«Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.»

http://ru.wikipedia.org/wiki/Момент_инерции

На тему массы уже было сказано. От перемены направления движения, изменения угла поворота, роль массы не меняется. Изменяются направления и импульсы составных частей. В круговом движении действует центробежное ускорение (центробежная сила) с его ростом изменяется распределение импульсов и их направлений. Меняется вес в итоге. Чем дальше удаление от оси, тем больше вес при постоянстве угловой скорости. Эффект «вращающегося фигуриста». Центробежная сила равноценна толкающей силе, в отличие от тянущей. В данном случае вращающееся на опоре тело не растягивается, а сжимается. Растягивается сама опора. Силы упругости направлены к оси не перпендикулярно, а под некоторым углом, который зависит от места их определения относительно места крепления, от угловой скорости.. Чем больше скорость, тем меньше угол. В результате распределение плотности внутри тела растет в зависимости от радиуса.

Классика введением центростремительной (фиктивной) силы попыталась через нее выразить силы упругости либо самого вращающегося тела, либо силы упругой связи. Что на поверку является нарушением закона Ньютона.

Касательный вылет тела при потере точки опоры(отрыв от оси) является только кажущимся эффектом, в виду отсутствия достаточных сил трения. При их присутствии, после отрыва, тело начинает вращаться и вылетает не по прямой, а по спирали, то есть не по касательной к окружности вращения.

http://fatyf.narod.ru/Magnus-effect.htm

Любая неоднородность в плотности среды вызывает этот эффект, а значит и не прямолинейное движение. Ярчайший пример это движение шарика - спираль на поверхности вращающегося диска.

Если тело движется по окружности либо вокруг собственной оси, то разбирать это движение надо не с позиции прямолинейного движения, а с позиции изменения угла поворота и скорости вращения.

И не точечного представления тела, обладающего массой.

Кинематика это слишком упрощенное объяснение физического процесса.

В осевом моменте инерции отсутствует скорость вращательного движения.

Поэтому само понятие осевого момента инерции представляет собой не вращательное движение, не динамику, а статику. И относится скорее к сопромату.

Основанные на таких расчетах представления о распределении плотности планет являются математической абстракцией не несущей достаточного для динамики физического смысла.

Частота вращения — число оборотов тела в единицу времени.

Момент силы относительно оси

«Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.»

Выдумка.

Есть работа по теме кинематики вращательного движения.

Тимофей Гуртовой

АЛЬТЕРНАТИВНАЯ ФИЗИКА БОЛЕЕ РАЦИОНАЛЬНА http://new-idea.kulichki.net/pubfiles/081127032328.doc

В этой статье довольно четко освещены проблемы вращательного движения и на мой взгляд достаточно корректно решен начальный этап теории вращательного движения с одним но.

Автор не смотря на все заявления все таки пользуется линейным представлением , описывая угловую скорость как сумму линейных векторов. А это не является до конца верным.

Надо использовать вектор как криволинейный с указанием радиуса кривизны и направления. Тогда появится и соответствие полное.

То есть скорость есть функция Rdф

Рассмотрим момент импульса.

«Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса»

Помимо того, что у импульса, как величины векторной уже имеется НАПРАВЛЕНИЕ, во вращательном движении это направление еще раз направляют на путь «истинный». И вводят «псевдовектор» - проекцию импульса на ось вращения. Мало того, опять заменяют скаляром. Масло масляное. Импульс на Косинус или Синус угла да еще две составляющие.

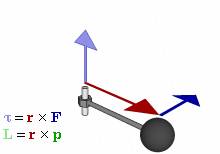
http://ru.wikipedia.org/wiki/Момент_импульса

Спрашивается, зачем это делается?

причина – попытка квантовой механики объяснить ларморовскую прецессию.

Собственно к механике Ньютона это отношения не имеет. Да и как импульс можно перенести на ось, тем более математическую, если он уменьшается с радиусом до нуля.

Вопрос пятый.

Перекликается с инерцией. Увеличивается ли масса при ускоренном движении. Нет в идеальном случае, как и по первому закону. С поправкой: на движущийся объект не должно действовать никакое излучение(либо любые механические действия) приводящее к изменению массы. Без оговорок.

Вопрос шестой.

Как все это увязать с законом Гука? Да, ешкин кот! Читать Ньютона надо. « книга 2 «Начала…. О движении тела с сопротивлением пропорциональному скорости….» мне пришлось пройти тот же путь и не читая полностью монографию. А Ньютон уже давно все сделал!!!!!!!!

F=-kx закон Гука.

Своего рода статистический закон. Фиксирует начальный и конечный момент движения пружины. Сама динамика заложена в формуле ньютона

mdv/dt=-kdx/dt где коэффициент жескости пружины не статичен и меняется только в узких границах. должен подчинятся тем же закономерностям.

сопротивление, а что это как не упругость среды.

Упругость тела до начала движения, и упругость среды во время движения. При отсутствии упругости среды работает сила упругости тела. Равномерное прямолинейное движение.

А упругость это и есть сила инерции. Вот только направление обратное направлению силы растягивания при отпускании пружины. Ну, и любое тело есть пружина.

Вот поэтому о инерции Ньютон ничего и не упоминал. И не надо было!!!!!

Мало того предусмотрел нелинейное возрастание сопротивления.

А Наша нынешняя наука и его последователи типа Кориолиса да Понселье похоже тоже как и я, целиком не удосужились прочитать «начала…» да их осмыслить….

Посмотрите, этой ньютоновской формулы mdv/dt=-kdx/dt ни в одном учебнике нет!!! В угоду официальному мнению!!!!!!!!! Зато есть силы инерции. А вот теорема Ньютона с учетом упругости из закона Гука или сопротивления правда касается это только среды, а самого тела, что не касается?

И продолжим о мере инерционности. Если мы начнем просто растягивать пружину, приводя ее в статическое состояние, в качестве силы мы получим вес(аналогию нашей любимой массы),

-kx=mg

и внешне не будет никакой динамики (хотя внутри она есть). Но если мы будем рассматривать сам процесс растягивания пружины, без законов Ньютона нам не обойтись.

Именно поэтому нельзя считать энергию пружины по формуле А=kx2/2, энергией будет сам вес, пропорциональный массе. Посмотрим на классику, как она понимает работу при растягивании пружины и видим то же самое что и в первом случае:

«Зависимость модуля внешней силы от координаты x изображается на графике прямой линией.» Сила приложена и действие уже совершено. Мы уже приложили силу и растянули пружину, хотя бы подвесив груз. Работа сделана!!!!! Какую еще надо?

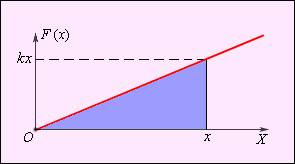
А что делается? «По площади треугольника можно определить работу, совершенную внешней силой, приложенной к свободному концу пружины: »

Еще один способ оправдания ½, вопрос зачем? Перемещение явно учтено дважды без всяких ухищрений с векторами.

И что дает площадь треугольника, ничего. Данный график зависимости силы от перемещения означает зависимость F/x = kx/x, то есть силу, деленную на перемещение.

Физически все точки на линии представляют собой коэффициент жесткости пружины и ничего более. Такой график просто не имеет физического смысла. И график, построенный таким образом для F=ma или F=mg будет показывать абсурдную зависимость массы от квадрата времени.

Пружина это аналог рычажных весов с плечом переменной длины, поэтому к нему относится все вышесказанное в пункте два.

И мерилом инерционности останется все равно сила. То бишь, килограмм. «А пуд как был, он так и есть – шестнадцать килограмм!»

Подвопрос. Выясняется неладное с потенциальной энергией тела поднятого на высоту h. E=mgh в связи с вышеизложенным. Какова кинетическая энергия свободно падающего тела? Вывод простой. Кинетическая полная энергия E=mg. Ускорение свободного падения изменяется в соответствии с законом гравитации Ньютона

Следствие.

И что получается? Приведенные мною выкладки в статье http://fatyf.narod.ru/electrostatics.htm,

Касающиеся закона Ома можно теперь целиком соотнести на ньютоновские законы движения.

Энергия электрического взаимодействия есть интеграл от силы тока по времени оно и есть механический импульс (который провода дергает, а дуга электросварки притягивает), Сопротивление это сила противодействия току. Сама сила тока скалярно и есть его энергия, растянута во времени и может поддерживаться бесконечно долго, то есть мощность. В то время как аккумуляция и расход энергии определяется временем расходования, совершенной работой, энергией, импульсом. Именно ее мы и используем во всех энергетических расчетах. Тяга это одно, а сила на время это другое….. Именно поэтому в русском языке лошадиная сила подразумевает мощность. А напряжение это потенциальная энергия. Что сразу убивает Максвелловскую «энергию» заряженного конденсатора, стремившегося подогнать формулу W=qC²/2 под вид формулы E=mc²/2

И все это при условии, если не принимать в учет малость и фактическую непонятность кванта энергии излучения по определению величины неопределенной... исходя из самих квантовых представлений (постоянная планка и есть тот самый принцип соотношения неопределенностей). То есть для измерения и понимания физических явлений, производимых излучением, в частности и электрическим током, вполне необходимо и достаточно значения сил вызываемых движением этого излучения. Остальную детализацию вплоть до фотона можно до лучших времен оставить в покое, а может и совсем забыть, покончить с насилием квантовой механики над здравым смыслом.

Данные выводы позволяют, например, простейшим образом объяснить движение проводников в большинстве опытов приведенных Николаевым Г.В. в его монографии «Непротиворечивая электродинамика. Теории. Эксперименты парадоксы.» Томск. Изд-во НТЛ. !997 г., http://doverchiv.narod.ru/Nikolaev/Nikolaev_modern_electrodynamics.htm

А также большую часть классических эффектов электродинамики, связанных с движением проводящих сред.

Единственно, что волнует это сама масса и связь массы с излучением. Когда мы массу считаем предметом материальным, а электромагнитное излучение считаем безмассовым(идеальным), но имеющим силу(энергию) f=ma при двух неизвестных, при этом имеем возможность превращать массу в (излучение+меньшая масса) и наоборот (излучение+большая масса) нам остается всего один шаг до определения этого понятия. Определить скорость излучения не по Лоренц-ейнштейновско-милликеновской технологии для каждого конкретного для каждой конкретной среды. И, наконец, экспериментально в весомых количествах получить вещество из излучения без заметного участия посторонней массы. Вот зачем необходима физика высоких энергий. При этом экспериментальных методик возможно предложить

достаточное количество, базируемых на уже известных эффектах электродинамики.

Поступим формально.

F=ma это не энергия, это сила. масса - это вес с безразмерным коэффициентом. вес исчисляется в единицах сравнения. В частях эталона. время и длина тоже.

Это Формальное определение силы.

у Фарадея не определение, а физический закон, им открытый. Закон электролиза.

тот же вес равен!!!!!количеству электричества, помноженному на время с безразмерным коэффициентом. m=kIt

все свойства массы в электричестве!!!!!!.

Свойство инерции уже зарыто в массе. А понятие импульса вроде уже достаточно.

p=mv, чтоб именно его считать энергией движущегося тела. Формулы в математике - формализм.

давайте вместо тока подставим импульс частиц(электронов) переносящих его энергию. и будем очень аккуратны с размерностями.

m=Kmvt (v=s/t), время сокращаем, m=Kms размерности поплыли, появился путь, но этот путь может кое как физически объясним. Это расстояние между электродами. Электричество перемещает массу. Вместо расстояния можно воткнуть безразмерные координаты и формально условие равенства станет выполнимо.

Вы, наверное, заметили, все таки есть неформальная часть, волюнтаризм. Ток действует определенное время, а импульс есть мгновенное значение силы. Интеграл от силы и значит: .

Надо подставлять силу.

M=kmat тогда получим m=kmv, а это реальное воплощение силы тока в массе выражение массы через массу с ее инерционными свойствами(импульс) и свойствами конкретного вещества, зависящими от данного тока.

А механическая сила вот тут и будет эквивалентна силе тока. Физически!!!!!

И математически!!!

Теперь подставим mv²/2 собственно энергию.

m=Ktmv²/2 сократим время, получим m=Kms²/2t кг м²/сек это уже физически необъснимо, площадь за секунду???? Да пусть и пространство-время!!!

Точно так же физически необъяснимо и E=mc² при размерности кг м²/t²

Точно так же физически необъяснима постоянная планка. Дж сек.

1 кг·м²/с

Да и сам джоуль.

Резюме.

Ошибки в классическом от Кориолиса и Понселье, понимании работы и энергии очевидны.

Нельзя учитывать путь дважды. ds ds/dt² да в угоду интегрированию добавлять ½.

Потеря косинуса угла приложения силы в классическом изложении..

Выводы.

Работа равна полной (кинетической) энергии и равна количеству движения или импульсу на малом прямолинейном участке.

Потенциальная (внутренняя) энергия заключена в массе.

F=ma сила

P=mv импульс

Третий закон ньютона в применении к силам упругости и трения:

kx=-mа

третий закон ньютона в применении к покоящемуся на опоре телу

-kx=mg

сила инерции это сила упругости движущегося тела и направлена по направлению движения.

Второй Закон Ньютона F=ma определят силу, полученную из уже известных исходных данных: УЖЕ!!!!! пройденного пути, скорости и ускорения по направлению движения.... именно это и отражает дифференциальная форма закона....он не занимается предсказанием траектории....

траекторию определяет другой закон Ньютона (третий): F1=-F2 знак неравенства в этой формуле...

тело равноускоренно двигается только при наличии дополнительной силы двигателя.... инерция не предусматривает такой силы....это внутренняя энергия тела, импульс, полученный во время применения силы. кроме сил упругости, реальных сил, могущих объяснить инерцию нет.

В данной постановке вопроса Эйнштейно-Лоренцевское инваринтно-относительное просто остается за бортом нашего теплохода… поскольку подобное кинематическое описание пространства xyzt без участия массы, ее плотности, силы, импульса исключается. И просто предлагается многофакторный анализ.

К тому же само неэвклидово пространство, описываемое геометрически, ставит физический параметр, время, в качестве единицы измерения…. Низводя его до абсолюта. Точно с таким же успехом можно и физический параметр массы применить в виде координаты. И строить график зависимости массы от перемещения. Что конечно не лишено физического смысла, но надо опытным путем убеждаться в этой и другой зависимости, а не строить математических фантазий, ожидая изотропности и абсолютности того, что мы наблюдаем.

Спас жилет не предлагается.

Ну и в заключение хочется вспомнить родную лошадиную силу как инструмент измерения мощности. Бедная лошадка, страгивая телегу с места и не подозревает, что по классике численно тратит гораздо больше энергии (сил), чем ей требуется на самом деле, и пашет она через силу.

P.S.

в сообществе Физика на блоге мой мир Mail@ru частенько выступает Семен Николаев. Мы с ним, бывает, спорим. И данная статья является одним из результатов этих споров.

Я целиком и полностью его поддерживаю в части того, что ничего не пытаясь менять, невозможна эволюция науки. Она постепенно будет превращаться в религию. И мало того в религию наслаивающихся друг на друга ошибок.

«Конечно, многим наплевать, что его заставляли учить ошибочные законы и формулы. А теперь заставляют делать это Ваших детей и внуков. Разрешить это положение может только ликвидация монополии РАН на научную истину.

Неужели Вы не видите по нашему форуму, как некоторые говорят, не нужно про процесс, пиши формулы. Другие думают, какую систему отсчёта применить для энергии. Они уже одурачены и запутаны.

А всё просто объясняется классическими механикой и электродинамикой.», Семен Николаев.

Добавлю от себя лично. КЛАССИКОЙ, не изуродованной безграмотными ремейками!!!!!!!

Мы все настолько привыкли к догмам, что не замечаем даже простейших ошибок.

Так же данным постскриптумом подводится черта под спорами с Владимиром Ерохиным, Виктором Кругловым , Игорем Шеиным. которым я безмерно благодарен за жаркую полемику в связи с данным вопросом.

Большое Спасибо Станиславу Петренко за поддержку и личный вклад, оказанный при написании статьи.

1. Ньютон Исаак. “Математические начала натуральной философии”. Перевод академика А.Н.Крылова. “Известия” Николаевской Морской Академии. Выпуск IV, V. Петроград. 1915 – 1916 гг. Книги I,II,III. 620 стр.

Фатьянов Александр Васильевич Спб 7-8 марта 2010

Fatyalink@mail.ru

Исправлено и дополнено 18, 29 марта 2010. с этой даты

Материал защищен, и копирование без ссылок на автора, а так же использование без ссылок материалов данной статьи будет преследоваться по закону.

Исправлено 31.10.2010, 4.02.2011 в части разбора кинематики равноускоренного движения,

Дополнения и уточнения 6.07.2011 общего плана.

В начало на лист изменений